The reverberations from the Lewis/Crok report are still playing out in the blogosphere. In particular there are some interesting comments at Ed Hawkins' blog.
One of the memes that is being pushed by our climatological friends is the idea that the Lewis/Crok range for transient climate response (i.e. short-term warming) is similar to that of the IPCC models. Myles Allen was the first to promote this idea, in his comments at the Science Media Centre.
Their 5-95% range of uncertainty in TCR (kindly provided by Nic Lewis) is 0.9-2.5 degrees C, almost exactly in line with the range of the models shown in their figure (1.1-2.6 degrees C).
This idea has now been repeated by Ed Hawkins:
Focussing on TCR, Lewis & Crok give a ‘likely’ range of 1.0-2.0K. The same IPCC AR5 range is 1.0-2.5K, taking into account other lines of evidence. The 5-95% ranges from Lewis & Crok are almost the same as the 5-95% ranges from the GCMs (Nic Lewis confirmed this to Myles Allen).
Well up to a point, Lord Copper. As Troy Masters - another independent scientist with publications in the area - has pointed out in the comments at Ed Hawkins' blog, a 5-95% range, being so wide, can hide a multitude of sins, including for example vastly different skews from one distribution to another.
...these ranges can be similar while at the same time the specifics of the actual distributions (median, mode, etc.) can be very different and have largely different policy/impact implications. You are right that the similarity in these ranges between Lewis and Crok and the IPCC report might make the distinction insignificant (although estimated impacts/costs are disproportionately affected by the upper bound) IF the IPCC did not imply knowledge of the distribution within that range of TCRs. However, while the report does not explicitly give a “most likely” value for TCR, it implicitly suggests one with the statement in the SPM that global surface temperatures are “more likely than not to exceed 2C [above pre-industial by 2100] for RCP4.5 (high confidence)”. This is based on the GCMs with an average TCR of 1.8 K, significantly higher than the estimated “most likely” value used in Lewis and Crok. Similarly, I think most people would agree that if TCR is 1.0 K and ECS is 1.5 K (both within the “likely” range of the reports), we are unlikely to hit that 2K target under RCP 6.0 by 2100, but again AR5 says “warming is likely to exceed 2C for RCP6.0…(high confidence)”, thereby implicitly assigning a low probability to the lower end of that range.
I don’t think the IPCC report can have it both ways. Either the SPM must say “we don’t know” about whether we are likely to exceed 2K under RCP4.5 and RCP6.0, because the likely range of TCRs include those that exceed or fall below this mark, or it must stop saying that estimates of TCR are consistent simply because the ranges are consistent (as those statements rely on more specific aspects of the distribution). Given that RCP4.5 includes increasing emissions up to 2040, and RCP6.0 increasing emissions up to 2060 (albeit neither at the rate of RCP8.5), consider the difference of the implications when using the IPCC implicitly assumed distribution of TCR estimates vs. the explicit most likely values of Lewis and Crok:
IPCC AR5 using implictly assumed TCR distribution: we are more likely than not to exceed 2K by 2100 under the scenario where emissions continue to increase up to 2040, and likely to exceed 2K under the scenario where emissions continue to increase up to 2060 (high confidence).
Lewis and Crok: we are unlikely to exceed 2K by 2100 under the scenario where emissions continue to increase up to 2040, and more likely than not to stay below 2K by 2100 under the scenario where emissions continue to increase up to 2060.
In both cases we might say the TCR ranges are the same, but they convey largely different messages to policy makers.
In fact it's worse than that, because although the IPCC's CMIP5 models have an average TCR of the order of 1.8°C, as Lewis and Crok point out in their report the amount of warming that the models predict is even higher than this number implies.
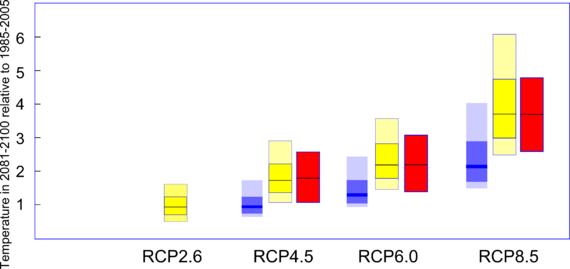
It is actually possible to show the very significant discrepancy between what the IPCC is telling policymakers and Nic Lewis's work, based on the AR5 forcing and heat uptake data and the observational studies. In Figure 12.8 of the Fifth Assessment, the IPCC reports the range of projected warming under the various RCP scenarios, including the 5-95% and 17-83% ranges as well as the medians. Nic Lewis has kindly sent me the equivalent projected figures, calculated using a two-box model and using the various key percentiles from the TCR and ECS ranges in his report. I have drawn these (in blue) next to the IPCC's figures (in red - main warming projections 17-83% ranges and means, based on the ensemble of CMIP5 models; in yellow - 5-95% and 17-83% ranges and medians from AR5 Figure 12.8, based on Rogelj et al 2012).*
The difference, as I'm sure you will agree, is pretty stark. But Lewis's results are, in climatological speak, "almost the same" as the IPCC's.
One last thing. I wondered how it was that Nic Lewis could have provided Myles Allen with the extra data about the range of his TCR estimate without the details of the skewness getting passed on too. Did he not pass on the likely range too?
I asked Nic about this. It turns out he provided Myles with the 'likely' range first, and Myles then asked for the 5-95% range. Nic was worried that quoting just the 5-95% range would mislead people. So he sent Myles the 5-95% range, stating that he was happy for Myles to quote it as long as he also gave his (Nic's) median and likely range.
Oh dear.
*Nic asks me to note the following caveats: The best estimates and likely ranges are not identical to those given in the Lewis and Crok report (although the TCR best estimate is virtually the same): the values given in the report have been made more conservative. The percentiles that these projections represent will only approximate the percentiles of the TCR and ECS values used, because some uncertainty is not common to TCR and ECS.